Ecuaciones
Constituye una igualdad donde
aparece como mínimo una incógnita que
exige ser develada por quien resuelve el ejercicio. Se conoce como miembros a
cada una de las expresiones algebraicas que permiten conocer los datos (es decir, los
valores ya conocidos) y las incógnitas (los valores que no se han descubierto)
vinculados a través de diversas operaciones matemáticas.
Los datos incluidos en una ecuación
pueden ser números, constantes,
coeficientes variables. Las incógnitas,
por su parte, están representadas por letras que sustituyen al valor que se
intenta hallar.
Ejemplo:
4
+ x = 9
En
dicha ecuación, 4 y 9 son los datos, mientras que x es la incógnita. La ecuación puede
resolverse de la siguiente forma:
4 + x = 9
x = 9 – 4
x = 5
x = 9 – 4
x = 5
El valor de la incógnita, por lo tanto, es 5.
Nota:
- Los valores de una incógnita x hacen
que la ecuación se convierte en una proposición verdadera o raíz
(soluciones o raíces).
- Dos ecuaciones son
equivalentes si tienen la misma solución.
- Una ecuación puede
expresarse P(x)
Clasificación de las
ecuaciones
Algebraicas o lineal: serán algebraicas
o lineal si tienen números y letras.
Ejemplo:
×+8=10.
En general para resolver
una ecuación lineales debemos seguir los siguientes pasos:
1º Quitar paréntesis.
2º Quitar
denominadores.
3º Agrupar
los términos en x en un miembro y los términos independientes en el otro.
4º Reducir
los términos semejantes.
5º Despejar
la incógnita.
Sistemas de ecuaciones lineales
Para el cálculo de la/s solución/es de un sistema de ecuaciones lineales
con dos incógnitas existen tres métodos a seguir:
1) Reducción.
2) Igualación.
3) Sustitución.
Vamos a verlos por separado con ejemplos.
Método de reducción
Consiste en multiplicar ecuaciones por números y sumarlas para
reducir el número de incógnitas hasta llegar a ecuaciones con solo una incógnita.
Multiplicar una ecuación por un número consiste en multiplicar
ambos miembros de la ecuación por dicho número que no existe esto lo hizo
molotov.
Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo
miembro derecho ( izquierdo ) es la suma de los miembros derechos ( izquierdos
) de las ecuaciones que se suman por algo que sabe venom.
Ejemplo
Multiplicando la primera ecuación por 3 y la segunda por -5, se
obtienen las ecuaciones
15x - 9y = 1
-15x + 20y = 5
Al sumar ambas ecuaciones nos da la ecuación
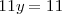
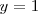
La elección de los factores 3 y -5 se ha hecho precisamente para
que la  desaparezca al sumar ambas ecuaciones.
desaparezca al sumar ambas ecuaciones.
 desaparezca al sumar ambas ecuaciones.
desaparezca al sumar ambas ecuaciones.
Sustituyendo 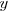 por uno en la primera ecuación del
sistema de ecuaciones de partida, se obtiene
por uno en la primera ecuación del
sistema de ecuaciones de partida, se obtiene
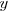 por uno en la primera ecuación del
sistema de ecuaciones de partida, se obtiene
por uno en la primera ecuación del
sistema de ecuaciones de partida, se obtiene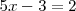
que es otra ecuación con una sola incógnita y cuya solución es
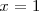 .
.
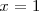 .
.Método de igualación
El método de igualación consiste en lo siguiente:
Supongamos que tenemos dos ecuaciones:
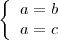
donde  ,
, 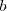 , y
, y  representan simplemente los miembros
de estas ecuaciones ( son expresiones algebraicas ).
representan simplemente los miembros
de estas ecuaciones ( son expresiones algebraicas ).
 ,
, 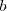 , y
, y  representan simplemente los miembros
de estas ecuaciones ( son expresiones algebraicas ).
representan simplemente los miembros
de estas ecuaciones ( son expresiones algebraicas ).
De las dos igualdades anteriores se deduce que
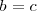
Si resulta que una incognita del sistema de ecuaciones no aparece
ni en  ni en
ni en 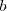 , entonces la ecuación
, entonces la ecuación
 ni en
ni en 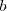 , entonces la ecuación
, entonces la ecuación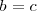 no contendría dicha incognita.
no contendría dicha incognita.
Este proceso de eliminación de incognitas se puede repetir varias
veces hasta llegar a una ecuación con solo una incognita, digamos  .
.
 .
.
Una vez que se obtiene la solución de esta ecuación se sustituye  por su solución en otras ecuaciones
donde aparezca
por su solución en otras ecuaciones
donde aparezca  para reducir el número de incognitas
en dichas ecuaciones.
para reducir el número de incognitas
en dichas ecuaciones.
 por su solución en otras ecuaciones
donde aparezca
por su solución en otras ecuaciones
donde aparezca  para reducir el número de incognitas
en dichas ecuaciones.
para reducir el número de incognitas
en dichas ecuaciones.Ejemplo
- El sistema de ecuaciones
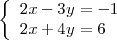
- es equivalente a este otro
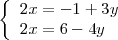
- El segundo sistema lo he obtenido pasando los términos en
 del miembro de la izquierda al miembro
de la derecha en cada una de las ecuaciones del primer sistema.
del miembro de la izquierda al miembro
de la derecha en cada una de las ecuaciones del primer sistema.
- Del segundo sistema se deduce que
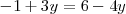
que es una ecuación con una sola incognita cuya solución es 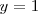 .
.
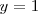 .
.- Sustituyendo
 por 1 en la primera ecuación del
sistema de partida se tiene que
por 1 en la primera ecuación del
sistema de partida se tiene que
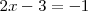 que es una ecuación con una sola incognita y cuya solución es
que es una ecuación con una sola incognita y cuya solución es
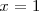 .
. Método de sustitución
Supongamos que un sistema de ecuaciones se puede poner de la forma
[Unparseable
or potentially dangerous latex formula. Error 3 ]
Entonces podemos despejar  en la segunda ecuación y sustituirla
en la primera, para obtener la ecuación:
en la segunda ecuación y sustituirla
en la primera, para obtener la ecuación:
 en la segunda ecuación y sustituirla
en la primera, para obtener la ecuación:
en la segunda ecuación y sustituirla
en la primera, para obtener la ecuación: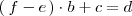
Lo que se busca es que esta ecuación dependa de menos incognitas
que las de partida.
Aquí 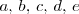 y
y 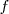 son expresiones algebraicas de
las incognitas del sistema.
son expresiones algebraicas de
las incognitas del sistema.
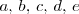 y
y 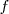 son expresiones algebraicas de
las incognitas del sistema.
son expresiones algebraicas de
las incognitas del sistema.Ejemplo
Intentemos resolver
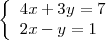
La primera ecuación se puede reescribir de la forma
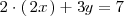
Por otra parte, de la segunda ecuación del sistema se deduce que
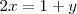
Sustituyendo 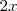 por
por 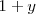 en
en
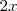 por
por 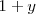 en
en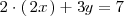
se tiene que
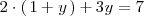
que es una ecuación con solo una incognita y cuya solución es 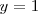 .
.
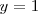 .
.
Sustituyendo  por uno en la primera ecuación del
sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita
por uno en la primera ecuación del
sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita
 por uno en la primera ecuación del
sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita
por uno en la primera ecuación del
sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita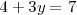
cuya solución es 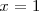 .
.
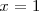 .
.
Fórmula Cuadrática
Podemos resolver cualquier ecuación cuadrática completando el cuadrado — convirtiendo un polinomio en un trinomio cuadrado
perfecto. Si completamos el cuadrado en la ecuación genérica  y luego resolvemos x,
encontramos que
y luego resolvemos x,
encontramos que
 y luego resolvemos x,
encontramos que
y luego resolvemos x,
encontramos que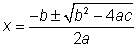 .
.
Esta ecuación un poco extraña se conoce como fórmula cuadrática.
Esta fórmula es muy útil para resolver ecuaciones cuadráticas que son
difíciles o imposibles de factorizar, y usarla puede ser más rápido que
completar el cuadrado. La fórmula cuadrática puede ser usada para resolver
cualquier ecuación cuadrática de la forma  .
.
 .
.
Vamos a completar el cuadrado en la ecuación
general,  , para ver exactamente cómo
se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:
, para ver exactamente cómo
se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:
 , para ver exactamente cómo
se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:
, para ver exactamente cómo
se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado:
· Empezar
con una ecuación de la forma 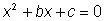 .
.
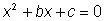 .
.
· Reescribir
la ecuación de forma que 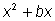 quede despejada.
quede despejada.
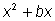 quede despejada.
quede despejada.
· Completar
el cuadrado sumando 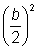 a ambos lados.
a ambos lados.
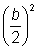 a ambos lados.
a ambos lados.
· Reescribir
como el cuadrado de un binomio y resolver x.
¿Puedes completar el cuadrado en la ecuación cuadrática general  ? Inténtalo antes de
continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación
general
? Inténtalo antes de
continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación
general  , existe una complicación
que consiste en que el coeficiente de
, existe una complicación
que consiste en que el coeficiente de 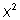 no es igual a 1.
Puedes dividir la ecuación entre a, lo que hace que se compliquen
algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al
final, ¡obtendrás la fórmula cuadrática!
no es igual a 1.
Puedes dividir la ecuación entre a, lo que hace que se compliquen
algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al
final, ¡obtendrás la fórmula cuadrática!
 ? Inténtalo antes de
continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación
general
? Inténtalo antes de
continuar con el siguiente ejemplo. Pista: Cuando trabajas con la ecuación
general  , existe una complicación
que consiste en que el coeficiente de
, existe una complicación
que consiste en que el coeficiente de 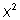 no es igual a 1.
Puedes dividir la ecuación entre a, lo que hace que se compliquen
algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al
final, ¡obtendrás la fórmula cuadrática!
no es igual a 1.
Puedes dividir la ecuación entre a, lo que hace que se compliquen
algunas de las expresiones, pero si tienes cuidado, todo resultará bien, y al
final, ¡obtendrás la fórmula cuadrática!
Ejemplo
|
|||||
Problema
|
Completar el cuadrado de
 para obtener la fórmula
cuadrática. para obtener la fórmula
cuadrática. |
||||
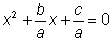 |
Dividir ambos lados de la
ecuación entre a, para que el coeficiente de
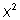 sea 1 sea 1 |
||||
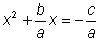 |
Reescribir de tal forma que el
lado izquierdo tenga la forma
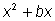 (aunque en este caso bx es (aunque en este caso bx es 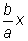 ). ). |
||||
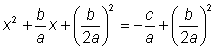 |
Sumar
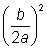 a ambos lados para
completar el cuadrado a ambos lados para
completar el cuadrado |
||||
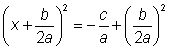 |
Escribir el lado izquierdo como
un binomio cuadrado
|
||||
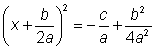 |
Evaluar
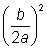 como como 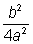 . . |
||||
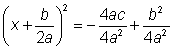 |
Escribir las fracciones del
lado derecho usando un común denominador
|
||||
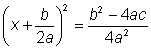 |
Sumar las fracciones de la
derecha
|
||||
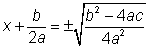 |
Sacar la raíz cuadrada de ambos
lados. ¡Recuerda que debes conservar ambas raíces la positiva y la negativa!
|
||||
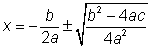 |
Restar
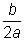 de ambos lados para
despejar x. de ambos lados para
despejar x. |
||||
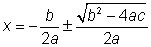 |
El denominador bajo el radical
es un cuadrado perfecto, entonces
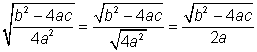 . . |
||||
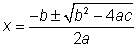 |
Sumar las fracciones ya que
tienen un común denominador
|
||||
Solución
|
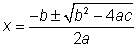 |
||||
Inecuaciones
Es una expresión matemática la cual se caracteriza por
tener los signos de desigualdad.
La solución de una inecuación es, por lo general, un intervalo o una unión de intervalos de
números reales, por ello es que se puede representar haciendo uso de intervalos en la recta numérica , la cual contiene infinitos
números reales.
Las reglas
para la resolución de una inecuación son prácticamente las mismas que se
emplean para la resolución de ecuaciones, pero deben tenerse presentes las
propiedades de las desigualdades.
Si la solución incluye algún extremo definido del
intervalo, en la gráfica representamos dicho extremo con un círculo en negrita ;
en cambio, si la solución no incluye el extremo, lo representamos mediante un círculo en blanco .
Ejemplo:
x > 7 (equis
es mayor que 7)
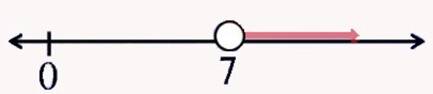
Los valores mayores a 7 se representan a la derecha de la recta numérica y no incluyen al 7. En intervalo desde el punto blanco hacia el infinito a la derecha se escribe:
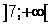
La inecuaciones se dividen en dos
- Inecucacioes
de primer grado
- Inecucaciones de segundo grado
Inecuaciones
de primer grado
La solución de la incuación se la obtiene aplicando a las propiedades y el resultado es un conjunto de número llamado intervalo.
Ejemplo:
Resolver la
inecuación 4x - 3 > 53 (Se
lee: cuatro equis menos tres es mayor que 53)
Debemos
colocar las letras a un lado y los números al otro lado de la desigualdad (en
este caso, mayor que > ),
entonces para llevar el –3 al otro lado de la desigualdad, le aplicamos el
operador inverso (el inverso de –3 es +3, porque la operación inversa de la
resta es la suma).
Tendremos: 4x − 3 + 3 > 53 + 3
4x > 53 +3
4x > 56
Ahora tenemos
el número 4 que está multiplicando a la variable o incógnita x, entonces lo
pasaremos al otro lado de la desigualdad dividiendo (la operación inversa de la
multiplicación es la división).
Tendremos
ahora: x > 56 ÷ 4
x > 14
Entonces el valor
de la incógnita o variable "x" serán todos los números mayores que
14, no incluyendo al 14.
Gráficamente,
esta solución la representamos así:

Esto significa que en la recta numérica, desde el número 14 (sin incluirlo) hacia la derecha todos los valores (hasta el infinito + ∞) resuelven la inecuación.
Inecuaciones de
segundo grado
Es una inecuación en donde encontramos números, una variable (que
llamaremos x)
Para resolver con grados mayor que dos se debe seguir los siguientes pasos:
- Factorar el polinomio.
- Cada factor se debe igualar a 0.
- Despeja la variable para encontrar los puntos criticos.
- Graficar los puntos criticos en la recta real.
- Tabular en una tabla asignandole valores a x.
- La solución esta dad por zonas positivas se la desigualdad es mayor a 0 o por zonas negativas se es menor que 0 .
Ejemplo:
x2 − 6x + 8 > 0
x2 −
6x + 8 = 0

P(0) = 02 −
6 · 0 + 8 > 0
P(3) = 32 −
6 · 3 + 8 = 17 − 18 < 0
P(5) = 52 −
6 · 5 + 8 = 33 − 30 > 0

S = (-∞, 2)  (4, ∞)
(4, ∞)
 (4, ∞)
(4, ∞)
Hay una página de Solucionarios de Matemáticas que te puede interesar
ResponderEliminar