Unidad 4

Dominio y rango de una función

El Dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida.

Es el conjunto formado por los elementos que tienen imagen. Los valores que le damos a x ( variable independiente) forman el conjunto original. Gráficamente lo miramos en el eje OX (abscisas), leyendo como escribimos de izquierda a derecha.

El Rango de la función es el conjunto de todos los valores que f toma.

Es el conjunto formado por las imágenes. Son los valores que toma la función "y" variable dependiente, por eso se denomina f(x), su valor depende del valor que le demos a "x". Gráficamente lo miramos en el eje OY (ordenadas), leyendo de abajo a arriba.

(En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución. Quizá también estos han sido llamados la entrada y salida de la función.)

Ejemplo:

Considere la función mostrada en el diagrama

 

Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D .

El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay letra en el dominio que se enlace con el 2.

Funciones Lineales

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).

.

Esta es la gráfica de la función lineal y = 3x + 2

Vemos que m = 3 y b = 2 (de la forma y = mx + b)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)

Ejemplo

 f(x) = 3x+2       Si x es 3,  entonces f (3) = 3*3+2 = 11

Si x es 4,  entonces f (4) = 3*4+2 = 14

Si x es 5,  entonces f (5) = 3*5+2 = 17

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 3 unidades. Si el valor de la pendiente es positivo la función es Creciente. Preste atención en que los valores de   x  y de  f(x)  NO SON PROPORCIONALES.

Lo que son proporcionales son los incrementos.

g(x) = -3x+7     Si  x= 0, entonces g (0) = -3*(0) +7 =   0+7 = 7

Si  x= 1, entonces g (1) = -3*(1) +7 = -3+7 = 4

Si  x= 2, entonces g (2) = -3*(2) +7 = -6+7 = 1

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades. Si el valor de la pendiente es negativo la función es Decreciente.

h(x) = 4             Si  x= 0   ,  entonces h(0)  = 4

Si  x= 98   entonces h(98) = 4

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje X.

Esta es la representación grafica de los tres tipos de funciones descritas.

Ejemplo

Representa gráficamente las siguientes funciones lineales  y = 2x  y  y = - 3x 18.2px; text-indent: 0px;">x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje X.

Esta es la representación grafica de los tres tipos de funciones descritas.

n>+ 4

Esta es la representación grafica de los tres tipos de funciones descritas.

Sugerencia: Primero elabora una tabla de valores, luego ubica los pares de puntos de la tabla en el plano cartesiano y finalmente únelos con una línea recta.

Los valores de x son asignados arbitrariamente o a tu gusto "te aconsejo usar valores pequeños para facilitar las operaciones" luego en la ecuación remplazamos la x por cada valor de la tabla. 

1.       y = 2x
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 2, y = 2(-2) = -4  quedando la pareja (-2 , -4)

       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)

pareja (-2 , -4)

       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)

span style='font-family:"Arial","sans-serif"'>       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

X	y = 2x
-2	-4
-1	-2
0	0
1	2
2	4

Función Cuadrática

Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax² + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.

Las gráficas de las funciones cuadráticas tienen características que están estrechamente relacionadas con su forma simbólica. A medida que exploremos estas gráficas, aprenderemos a identificar estas características, y veremos algunas de las maneras de estructurar las ecuaciones cuadráticas.

Graficando con Puntos

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

La función cuadrática más básica y simple tiene la ecuación . Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

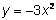
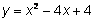
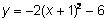
La función cuadrática más básica y simple tiene la ecuación . Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) 

   no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

x	y = x2
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:

 

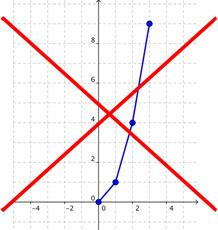
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.

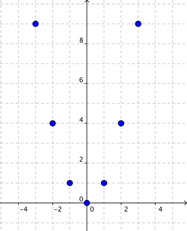
Borremos esas líneas rectas y grafiquemos el resto de los puntos:

no representa la función.

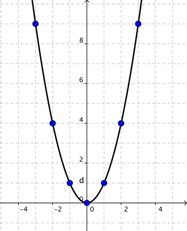
Una función cuadrática resulta en una gráfica con forma de U, llamada parábola. Los valores de la función cambian suavemente, por lo que la curva debe ser suave también. Ahora que podemos ver la naturaleza de la parábola (forma de U), veamos su forma en detalle.