Sistema cartesiano tridimensional
Un objeto es
tridimensional si tiene tres dimensiones. Es decir cada uno de sus puntos
puede ser localizado especificando tres números dentro de un cierto rango. El
sistema tridimensional mas usado en física (clásica) es el espacio: una
dimensión para el ancho, otra para la altura y otro para la profundidad. Para
representarlo basta con el gráfico de ejes cartesianos X,Y,Z. En las imágenes
se puede observar el gráfico con el que se representan los sistemas
tridimensionales.






Tipos de poliedros
Poliedro convexo

En un poliedro convexo una recta sólo pueda cortar a su superficie en dos puntos.
Poliedro cóncavo

Tetraedro


Hexaedro o cubo


Octaedro


Dodecaedro


Icosaedro


Poliedros irregulares


 Cuando hablamos de figura geométrica, lo hacemos en dos dimensiones (2D): largo y ancho, pero cuando hablamos de un cuerpo geométrico lo hacemos en tres dimensiones (3D) largo, ancho y alto. Es así como dejamos de hablar de una geometría plana, para introducirnos en el estudio de una geometría espacial. En la figura podemos observar, gráficamente, la diferencia entre ambos objetos matemáticos.
Cuando hablamos de figura geométrica, lo hacemos en dos dimensiones (2D): largo y ancho, pero cuando hablamos de un cuerpo geométrico lo hacemos en tres dimensiones (3D) largo, ancho y alto. Es así como dejamos de hablar de una geometría plana, para introducirnos en el estudio de una geometría espacial. En la figura podemos observar, gráficamente, la diferencia entre ambos objetos matemáticos.

- · Las coordenadas del punto E de la figura son (x,y,z).
- · La distancia signada x se llama abscisa, y se llama ordenada y z se llama cota.
- · Los planos coordenados dividen al espacio en ocho regiones llamadas octantes.
- · Los signos de las coordenadas se ilustran en la siguiente figura:

SISTEMA DE COORDENADAS
TRIDIMENSIONAL
Un sistema cartesiano tridimensional está compuesto
por tres planos perpendiculares entre sí, los cuales se interceptan en los ejes
coordenados, los que se denominan ejesOx,Oy yOz. Las coordenadas de un puntoP
son (x, y, z). La distancia signadas como x, y y z se llaman abscisa, ordenada
y cota respectivamente. Los planos coordenados dividen al espacio en ocho
regiones llamadas octantes.

También se puede emplear la regla de la mano
izquierda, como puede verse, los dedos medio, índice y pulgar se colocan en
direcciones perpendiculares entre sí, se nombran los ejes a partir del dedo
medio en orden alfabético.

Esta es la forma mas usual de
representar los sentidos positivos de los ejes cordenados

EJERCICIOS:
Poliedros
Un poliedro es la región del espacio limitada
por polígonos.

Caras
Las caras de un poliedro son
cada uno de los polígonos que limitan al poliedro.
Aristas
Las aristas de un
poliedro son los lados de las caras del
poliedro. Dos carastienen una arista en común.
Vértices
Los vértices de un
poliedro son los vértices de cada una de las caras del poliedro. Tres
caras coinciden en un mismo vértice.
Ángulos diedros
Los ángulos diedros están
formados por cada dos caras y tienen una arista en común.
Ángulos poliédricos
Los ángulos poliédricos están
formados por tres o más caras del poliedro y
tienen un vértice común.
Diagonales
Las diagonales de un
poliedro son los segmentos que unen dos
vértices no pertenecientes a la misma cara.
Tipos de poliedros
Poliedro convexo

En un poliedro convexo una recta sólo pueda cortar a su superficie en dos puntos.
Poliedro cóncavo

En un poliedro
cóncavo una recta puede
cortar su superficie en más de dos puntos, por
lo que posee algún ángulo diedro entrante.
Poliedros regulares
Un poliedro regular tiene todos sus ángulos diedros y todos sus ángulos poliedros igualesy sus caras son polígonos regulares iguales.
Sólo
existen cinco
poliedros regulares:
Tetraedro


Su superficie está formada por 4 triángulos equiláteros
iguales.Tiene cuatro vértices y cuatro aristas.Es una pirámide triangular regular.
Hexaedro o cubo


Su superficie está constituida por 6 cuadrados..
Tiene 8 vértices y 12 aristas..
Es un prisma cuadrangular regular. .
Octaedro


Su superficie consta de ocho triángulos equiláteros.
Tiene 6 vértices y 12 aristas.
Se puede considerar formado por la unión, desde sus
bases, de dos pirámides cuadrangulares regulares iguales.
Dodecaedro


Su superficie consta de 12 pentágonos regulares.
Tiene 20 vértices y 30 aristas.
Icosaedro


Su superficie consta de veinte triángulos equiláteros.
Tiene 12 vértices y 30 aristas.
Poliedros irregulares
Un poliedro irregular está
definido por polígonos que no son
todos iguales.
CLASIFICACIÓN DE LOS POLIEDROS POR SU NUMERO DE CARAS
| Nombre | Número de caras |
|---|---|
| tetraedro | 4 |
| pentaedro | 5 |
| hexaedro | 6 |
| heptaedro | 7 |
| octaedro u octoedro | 8 |
| eneaedro o nonaedro | 9 |
| decaedro | 10 |
| endecaedro o undecaedro | 11 |
| dodecaedro | 12 |
| tridecaedro | 13 |
| tetradecaedro o tetracaidecaedro | 14 |
| pentadecaedro o pentedecaedro | 15 |
| hexadecaedro | 16 |
| heptadecaedro | 17 |
| octadecaedro u octodecaedro | 18 |
| eneadecaedro o nonadecaedro | 19 |
| icosaedro o isodecaedro | 20 |
| triacontaedro | 30 |
| tetracontaedro | 40 |
| pentacontaedro | 50 |
| hexacontaedro | 60 |
| heptacontaedro | 70 |
| octacontaedro u octocontaedro | 80 |
| eneacontaedro o nonacontaedro | 90 |
| hectaedro | 100 |
| chiliedro | 1000 |
| miriedro | 10000 |
| decemiriedro | 100000 |
| hectamiriedro o megaedro | 1000000 |
| apeiroedro | ∞ |
Teorema de Euler
C + V = A + 2
| Nombre | Cara | Nº de caras | Nº de vértices | Nº de aristas |
|---|---|---|---|---|
| Hexaedro o cubo | Cuadrado | 6 | 8 | 12 |
| Tetraedro | Triángulo | 4 | 4 | 6 |
| Octaedro | Triángulo | 8 | 6 | 12 |
| Icosaedro | Triángulo | 20 | 12 | 30 |
| Dodecaedro | Pentágono | 12 | 20 | 30 |
EJERCICIOS
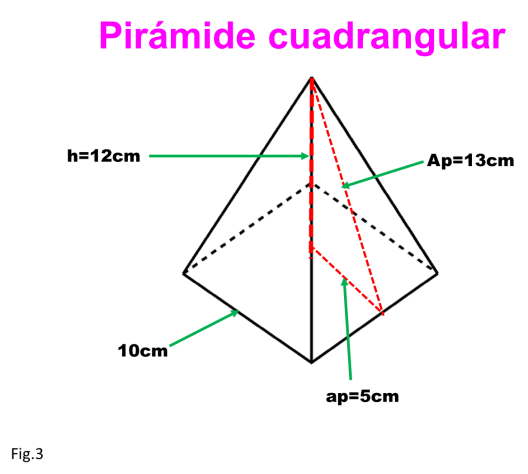
1.- Hallar el área total y el volumen de una pirámide cuadrangular cuya arista de la base mide 10, la altura de 12 cm y un Apotema del poliedro de 13 cm.
Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema
indica que es una pirámide cuadrangular con las siguientes medidas:
Obtengamos primero el área lateral (el de las cuatro caras triangulares) que es el área coloreada.
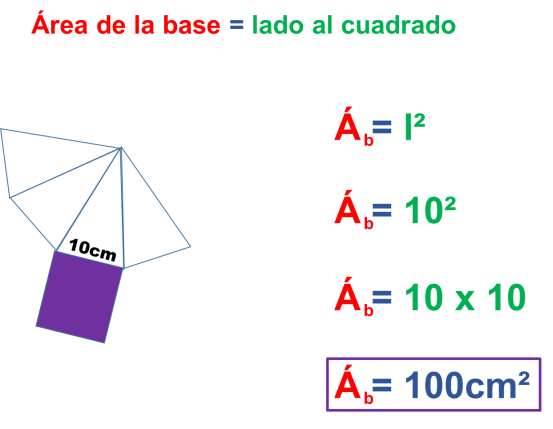
Y ahora el área de la base. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un cuadrado, ya que la base es cuadrangular. Es el área coloreada.
Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide cuadrangular especificada.
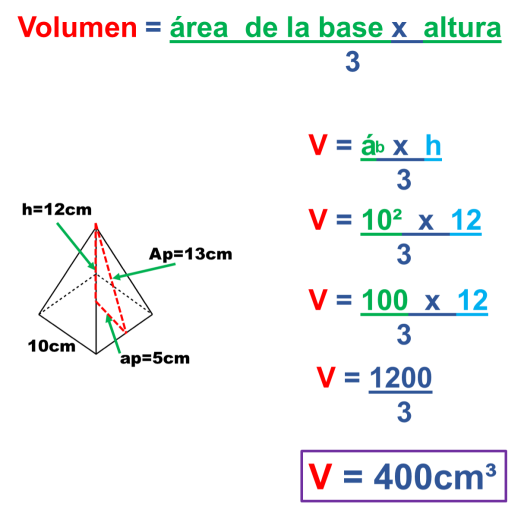
Ahora obtenemos el volumen de la pirámide cuadrangular sustituyendo la fórmula del área de la base por la del área del cuadrado y multiplicando por la altura del poliedro.
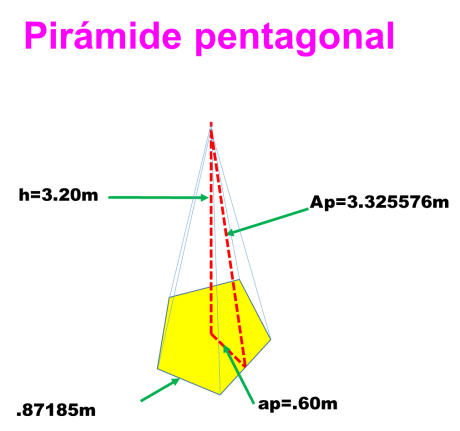
2.- Hallar el área total y el volumen de una pirámide regular pentagonal cuya altura mide 3.20m, el lado de la base 0.87185m, el apotema del poliedro 3.25576m; y el apotema de la base 0.60m
Nos enfocamos en la forma de la base de la pirámide para despejar estas fórmulas. El problema indica que es una pirámide pentagonal con las siguientes medidas.
Obtengamos primero el área lateral (el de las cinco caras triangulares) que es el área coloreada.
Y ahora el área de la base. Para ello en la fórmula general vamos a sustituir por la fórmula para obtener el área de un pentágono regular, ya que la base es pentágono. Es el área coloreada.
Por último sumamos los valores del área lateral y del área de la base para obtener el área total de la pirámide pentagonal especificada.
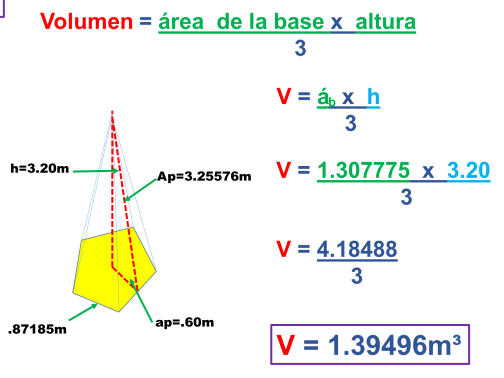
Ahora obtenemos el volumen de la pirámide pentagonal sustituyendo la fórmula del área de la base por la del área del pentágono y multiplicando por la altura del poliedro.
VOLÚMENES DE SÓLIDOS DE REVOLUCIÓN
Los sólidos de revolución son sólidos que se generan al girar
una región plana alrededor de un eje. Por ejemplo: el cono es un sólido que
resulta al girar un triángulo recto alrededor de uno de sus catetos, el
cilindro surge al girar un rectángulo alrededor de uno de sus lados.
Puede obtenerse mediante una operación geométrica de rotación
de una superficie plana alrededor de una
recta que se contenida en su mismo plano. En principio, cualquier cuerpo con simetría axial o cilíndrica es
un sólido de revolución.
Se denomina sólido de revolución o volumen de
revolución, al sólido obtenido al rotar una región
del plano alrededor
de una recta ubicada
en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje
de revolución.
Sea f una función continua y positiva en el intervalo
[a,b]. Si la región R indicada en la figura rota alrededor del eje X, ésta
genera un sólido de revolución cuyo volumen tratamos de determinar.

Rotaciones alrededor de los ejes cartesianos
El volumen de los sólidos generados por revolución alrededor de los ejes cartesianos se pueden obtener mediante las siguientes ecuaciones cuadráticas.
Rotación paralela al eje (x)
El volumen de un sólido generado por el giro de un área comprendida entre dos gráficas, f(x) y g(x) definidas en un intervalo [a,b] alrededor de un eje horizontal, es decir, una recta paralela al eje OX de expresión y=K siendo K constante, viene dado por la siguiente fórmula genérica
En particular, si se gira una figura plana comprendida entre y = f(x), y = 0, x = a y x = b alrededor del eje OX, el volumen del sólido de revolución viene generado por la fórmula:
método de discos.
Ambas expresiones se deducen de que al hacer girar un área formada por innumerables rectángulos de base dxy altura f(x), alrededor del eje X, se forman discos colocados verticalmente cuyos volúmenes sumados resultan en el volumen de todo el sólido. Cada disco tiene por volumen el de un cilindro como si fuera una moneda acomodada verticalmente, es decir, V=Πr²h donde el radio de la base del cilindro es f(x), y la altura del cilindro es dx, por lo que el volumen del cilindro resulta ser V = πf²(x)dx y la suma de todos estos volúmenes parciales, es el volumen total que resulta en la expresión:
Si son dos funciones f(x) y g(x), el volumen total será la resta del volumen mayor menos el volumen menor
Pero si el giro es alrededor de una recta paralela al eje X: y=K, entonces la expresión resultante es (siempre que K<X en para todo X):
en el caso en el que K>X, es decir la recta y=K que se encuentre debajo de las funciones, se debe aplicar:
Rotación paralela al eje de ordenadas (Eje y)
Éste es otro método permite la obtención de volúmenes generados por el giro de un área comprendida entre dos funciones cualesquiera, f(x) y g(x), en un intervalo [a,b], con f(x) > g(x) en el intervalo [a,b].Alrededor de un eje de revolución paralelo al eje de ordenadas cuya expresión es x=K siendo K constante positiva. La fórmula general del volumen de estos sólidos es:
Nótese que , por ende, esta fórmula funciona si la recta se encuentra a la izquierda de la región R comprendida entre las curvas f(x) y g(x), para que nuestra integral sea positiva.
Esta fórmula se simplifica si giramos la figura plana comprendida entre y=f(x), y=0, x=a y x=b alrededor del eje OY, ya que el volumen del sólido de revolución viene generado por:
EJERCICIOS:(método de cilindros o capas)
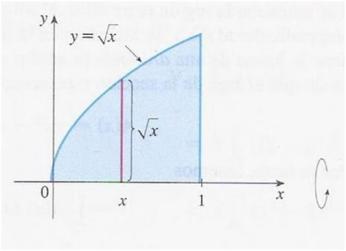
1) Hallar el volumen del solido obtenido al hacer girar alrededor del eje x la región bajo la curva:
y = √x, de 0 a 1.
y = √x, de 0 a 1.
-solución:
el solido está entre x=0 y x=1, graficamos y sacamos un disco (disco rosado).
el solido está entre x=0 y x=1, graficamos y sacamos un disco (disco rosado).
El volumen de este disco será:
V= π (√x)² = πx
2) Encuentre el volumen del solido obtenido al hacer girar la región limitada por
 , y
, y  , alrededor del eje y.-solución:
, alrededor del eje y.-solución:
 , y
, y  , alrededor del eje y.-solución:
, alrededor del eje y.-solución:
Graficamos y sacamos el disco (disco rosado):
el volumen de este disco será:
Poliedros y cuerpos redondos

Para empezar miremos cuales son las diferencias entre una figura geométrica y un cuerpo geométrico o poliedro.
 Cuando hablamos de figura geométrica, lo hacemos en dos dimensiones (2D): largo y ancho, pero cuando hablamos de un cuerpo geométrico lo hacemos en tres dimensiones (3D) largo, ancho y alto. Es así como dejamos de hablar de una geometría plana, para introducirnos en el estudio de una geometría espacial. En la figura podemos observar, gráficamente, la diferencia entre ambos objetos matemáticos.
Cuando hablamos de figura geométrica, lo hacemos en dos dimensiones (2D): largo y ancho, pero cuando hablamos de un cuerpo geométrico lo hacemos en tres dimensiones (3D) largo, ancho y alto. Es así como dejamos de hablar de una geometría plana, para introducirnos en el estudio de una geometría espacial. En la figura podemos observar, gráficamente, la diferencia entre ambos objetos matemáticos.
Los poliedros se relacionan estrechamente con las figuras planas, ya que un cuerpo geométrico está compuesto por caras que tienen forma de figuras planas o polígonos, como normalmente las conocemos. Es así entonces que definimos a los poliedros de la siguiente manera: Un poliedro es la región del espacio delimitada por polígonos. Lo poliedros o sólidos geométricos son figuras en tres dimensiones que poseen dos propiedades: el área de la superficie y el volumen. Los cuerpos geométricos se dividen en cuerpos redondos y poliedros.
Podemos reconocer una anatomía de los poliedros así:
- Cara: cada uno de los polígonos que forman el poliedro
- Aristas: Línea que se forma donde se unen dos caras
- Vértices: Punto donde se cortan tres aristas.
- Ángulos diedros: Ángulo formado por dos caras que tienen una arista en común.
- Ángulo poliedro: Ángulo formado por tres o más caras que tienen un vértice en común.
- Diagonal: Recta que une dos vértices de caras diferentes
Quedan por nombrar otros elementos que se irán estudiando con el paso del tiempo y que tienen que ver con algunas condiciones particulares de cada grupo de cuerpos geométricos.
Miremos ahora una breve clasificación de poliedros. Empecemos por los más estudiados que son los poliedros regulares o sólidos platónicos, recordemos que se llaman así porque todas sus caras son polígonos regulares.
Los primas y pirámides reciben sus nombres según la forma poligonal de sus bases, miremos algunas de ellas
Luego de mirar los anteriores cuerpo geométricos observemos un poco sobre qué es o qué son los cuerpos redondos. Estos son sólidos limitados por regiones curvas o planas y curvas, es decir, son aquellos que tienen al menos una de sus caras de forma curva; también se llaman cuerpos de revolución porque pueden obtener a partir de una figura alrededor de un eje.
EJERCICIOS
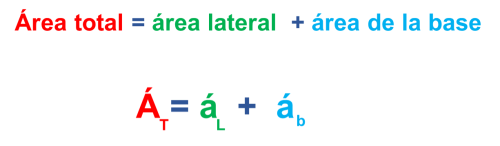





![{\displaystyle V=\pi \int _{a}^{b}([f(x)-K]^{2}-[g(x)-K]^{2})\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a680eae906e53485795cba741d911d75bd46dd6e)


![{\displaystyle V=\pi \int _{a}^{b}([f(x)]^{2}-[g(x)]^{2})\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c57aeb90c1077fdb5dfebab558db188172670c)
![{\displaystyle V=\pi \int _{a}^{b}([K-f(x)]^{2}-[K-g(x)]^{2})\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d31ea22334f9d49ae451d9d7a24c0f70ca1175d)
![{\displaystyle V=2\pi \int _{a}^{b}(x-k)[f(x)-g(x)]\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/477e11b211dce5af27a3f987c17a6bfd540478f2)



















No hay comentarios:
Publicar un comentario